One of the more simple and useful tools for determining passive component (resistance/capacitance/inductance) interactions is log-scale reactance paper (impedance paper, reactance normograph, etc.).
Here is an 8.5x11" printable sheet.
How does one use reactance paper? Use the following rules:
Impedance Shape:
- Resistance is a straight line at the value shown on the axis
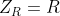
- Capacitance is a diagonal line, decreasing 20dB per decade - i.e. top left to bottom right
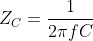
- Inductance is a diagonal line, increasing 20dB per decade - i.e. bottom left to top right
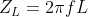
Impedance Combination (Magnitude):
- Series combination of two impedances
- As an approximation, when the impedances are not close in value, whichever line is higher (larger impedance) will dominate.
for 
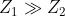
- Example (Resistor Green, Capacitor Blue, Combined Red Dash):
- Parallel combination of two impedances
- As an approximation, when the impedances are not close in value, whichever line is lower (smaller impedance) will dominate.
- Example (Resistor Green, Capacitor Blue, Combined Red Dash):
- Reciprocal
- The reciprocal of impedance
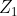is found simply by mirroring/flipping the impedance (vertically) over the horizontal line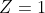 
- Multiplication and Division
- Division of two impedances
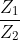is performed by plotting the difference between the two impedances because in a log-log (bode) plot,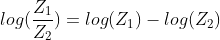 
- If the numerator is below (less than) the denominator, the line is below 0dB (
)
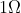- If the numerator is above (greater than) the denominator, the line is above 0dB
- If the numerator is increasing with respect to the denominator as frequency increases, the slope of the difference should be increasing.
- If the numerator is decreasing with respect to the denominator, the slope of the difference should be decreasing.
- Voltage Divider
- This is a specific useful case of series/parallel and division combination.
- For a dividing network
and 
, by multiplying both top and bottom by 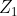one can see this is equivalent to 
where the second grouping 
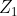is simply the parallel combination of and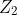 
.
- Therefore the divider impedance can be found by the parallel combination of
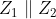and then plotting the difference between that impedance line and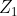
- As an example, consider the divider below:
The first step is to compute the parallel impedance (shown in red):
The next is to compare the numerator to the denominator
And plot the difference between the curves (with 0 difference corresponding to 0dB, or
).
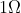
- Resonance
- Another useful specific case is to determine approximate damping resistance to avoid LC resonance. For a particular LC combination (e.g. Series 10mH with 1uF), the resonance point can easily be determined from the graph.
With ideal components, the impedance at the crossover resonance is
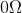
for series combination, and
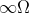
for parallel combination. To avoid a series resonance in the above case, a 100 ohm series resistance can be introduced to damp the resonance.
All of this can be done in a SPICE simulator or by hand via calculation, however I find the graphical approach to be a handy tool to do quick estimates (e.g. low-pass RC bandwidth or resonance damping as shown above), and to understand how passives interact in complicated networks to be able to intelligently adjust parameters for the desired effect.
Matlab Impedance Plot Code
Below is an example of plotting reactances in MATLAB. The code plots a user-defined capacitance, inductance, and resistance as well as reference lines. The number of reference lines and the axis scale is configurable.
close all;
clear all;
C_usr=10e-6; % Plot User-Specified Capacitance in Heavy Blue
L_usr=10e-9; % Plot User-Specified Inductance in Heavy Blue
R_usr=3e-1; % Plot User-Specified Resistance in Heavy Blue
Z_min=1e-3; % Minimum Y-Axis Value
Z_max=1e7; % Maximum Y-Axis Value
f_min=100; % Minimum X-Axis Value
f_max=1e9; % Maximum X-Axis Value
C_min=100e-12; % Minimum Reference Capacitance Plotted (One Reference per Decade)
C_max=1000e-6; % Maximum Reference Capacitance Plotted
L_min=1e-9; % Minimum Reference Inductance Plotted (One Reference per Decade)
L_max=1e-3; % Maximum Reference Inductance Plotted
% Distribute frequencies logarithmically between min/max
f=logspace(log10(f_min),log10(f_max),log10(f_max/f_min)+1);
% Distribute impedances logarithmically between min/max
Z=logspace(log10(Z_min),log10(Z_max),log10(Z_max/Z_min)+1);
% Distribute capacitances logarithmically between min/max
C=logspace(log10(C_min),log10(C_max),log10(C_max/C_min)+1);
% Distribute inductances logarithmically between min/max
L=logspace(log10(L_min),log10(L_max),log10(L_max/L_min)+1);
% Calculate Decade Constant-Capacitance Lines
Zc=zeros(length(C),length(f));
for i=1:length(C),
for j=1:length(f),
Zc(i,j)=1/(2*pi()*f(j)*C(i));
end
end
% Calculate decade Constant-Inductance Lines
Zl=zeros(length(L),length(f));
for i=1:length(L),
for j=1:length(f),
Zl(i,j)=(2*pi()*f(j)*L(i));
end
end
% Calculate user impedance lines
Zc_usr=zeros(1,length(f));
for j=1:length(f),
Zc_usr(j)=1/(2*pi()*C_usr*f(j));
end
Zl_usr=zeros(1,length(f));
for j=1:length(f),
Zl_usr(j)=(2*pi()*L_usr*f(j));
end
Zr_usr=zeros(1,length(f));
for j=1:length(f),
Zr_usr(j)=R_usr;
end
% Create a figure and plot
fig = figure;
loglog(f,Zc,':c','LineWidth',2);
hold on; % Overlay remaining plotted lines
loglog(f,Zl,':g','LineWidth',2);
loglog(f,Zc_usr,'LineWidth',2);
loglog(f,Zl_usr,'LineWidth',2);
loglog(f,Zr_usr,'LineWidth',2);
grid on; % Show logarithmic reference lines
axis([f_min,f_max,Z_min,Z_max]); % Scale Axis
% Labels
xlabel('Frequency (Hz)');
ylabel('Impedance (Ohms)');
hold off;
% Label Reference Capacitances at edge of plot
for i=1:length(C),
text(f(1),Zc(i,1),[num2str(1e6*C(i)),'uF']);
end
% Label Reference Inductances at edge of plot
for i=1:length(L),
text(f(length(f)),Zl(i,length(f)),[num2str(1e6*L(i)),'uH']);
end
is 
. 
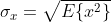
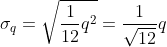
, or the noise level of the signal is greater than 1/2 a quantization step.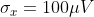
. 
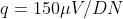(where 
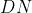stands for "digital number" or count).
apparent noise post-quantization versus 
.
