The effect of quantization is to add a uniform quantization noise distribution (convolve the input PDF with a uniform quantization noise PDF) and then apply a pulse train to the continuous convolved distribution.
The above paper shows how the resulting distribution's relationship in variance is the sum of the original variance with the variance of the uniform quantization PDF, which for a uniform distribution of width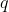 
is 
.
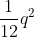The addition of variances
is equivalent to the quadrature (root-sum-square) combination of standard deviations as
where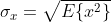 
and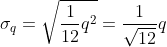 
(which incidentally is the same methodology as combining/adding independent Gaussian noise sources of varying standard deviations, as variances add)
B. Widrow et. al. "A Study of Rough Amplitude Quantization by Means of Nyquist Sampling Theory" and the previously mentioned paper demonstrate that the correlation of quantization noise remains low for relatively high input sample correlation (up to around 80%) so long as 
, or the noise level of the signal is greater than 1/2 a quantization step.
This conclusion about the distribution of quantization noise can be somewhat surprising as an individual quantization operation is a purely deterministic (completely correlated) operation on the input signal.
As an example, consider an electrical signal with uncorrelated white noise with a standard deviation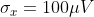 
.
This signal is quantized with a step size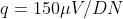 
(where 
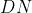stands for "digital number" or count).
The quantized distribution of samples would be expected to have a standard deviation of 
apparent noise post-quantization versus 
.
I verified this approximation in excel using 10,000 monte-carlo trials (see histograms below). The post-truncation standard deviation was 108.85, which is around 0.1% error.
The mean has shifted by -0.5DN due to the "floor" function applied during quantization.
